Published on: October 16, 2023
Author: Andrew Della Vecchia
Introduction
This is a continuation of the various discussions and exploration of random numbers. In part 1 of this series, we explored random numbers and the basics of generation. In part 2, we will investigate possible methods that can be used to measure the quality of a Random Number Generator (RNG). My initial thinking is that this is not a direct process and requires a good deal of rigor.
The question being asked is “are there any tests that come up with the ultimate decision of whether a RNG is worth using?” Is there a single test that determines this or is this a situation where a battery of tests is run? Are there any standards to measures? Will all the testing techniques currently known be enough to rely on for an answer?
I will start off this study with basic data exploration analysis. This will include reviewing the generated numbers directly, calculating a summary for the set, and analyzing the distribution. I will then execute analysis from techniques found from various sources1,2. Along the way, experimentation will be done. Hopefully, the path I take will provide some help in your analysis too.
Setup
To get the process started, I will pick a RNG and generate output for testing. Since I used the Mersenne Twister with Python for the previous article, I will use that algorithm to generate output as the basis for experiments in this article. I will let the seed be picked on its own by the system. The code for this step is in the appendix below.
I used integers in part 1 of this series but will switch to a float point value this time. The reason behind the switch to floats will hopefully become clear as experimentation goes on. The output is a file composed of 100,000,000 floating-point random numbers to be used. That count is one I picked due to processing limits on available system resources.
General Statistics
The initial step in data exploration is to take a basic look at some generated numbers from the file. Initially, I see that the floating-point values look complicated enough to make it difficult to predict.
[1] 0.88522728 0.08111702 0.42921423 0.49197895 0.81093116 0.73210104The following is a generated summary of the entire list:
min Q1 median mean Q3 max
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.00000000445 0.250 0.500 0.500 0.750 1.00
Those values look pretty much on point with expectations. There is no perfect 0 but the minimum value is quite small.
What about the spread of data?
> sd(standard_rng$random_number)
[1] 0.288676
That measure suggests the spread will be even from 0 to 1.
Are there any duplicates at all in this file?
This is a very simple test to run.
sum(duplicated(standard_rng$random_number))
[1] 1The results are straightforward that there is 1 duplicate. That is a good sign for a RNG that does not recycle itself much at all.
Experiment – Bin the Set
Before it gets boring, I will shake the tree (just a little bit). What happens if the set is put into wide bins at each 0.1 distance? If there is a heavy-handed area of the range found, that would indicate there is a possible pattern to the underlying RNG. Time to build a histogram. Is there an even distribution? Looking at the plot directly, the set seems to be evenly distributed:
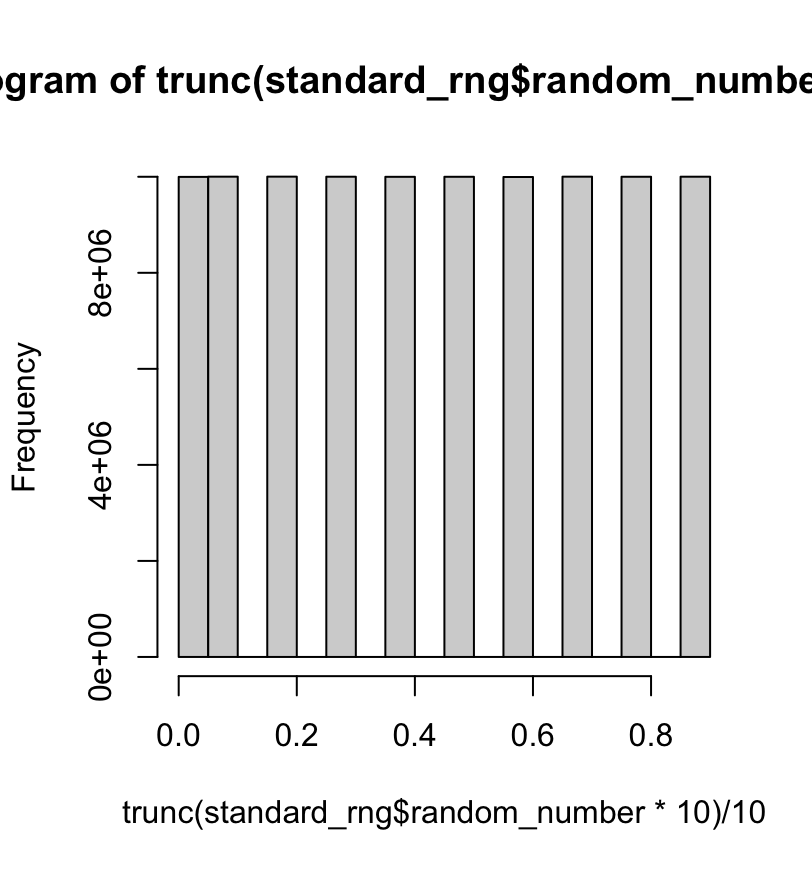
Looking at the finer detail, there are some small variations shown:
$counts
[1] 9997501 10001954 0 10002463 0 10000956 0 9999007 0 9999672 0 9995196 0 10001856
[15] 0 10000149 0 10001246
Not that much variation with the eye-ball test but still some differences between the bins.
Maybe a chi-squared can give a bit more of a definition to the distribution.
Chi-squared test for given probabilities
data: table(tr_rng)
X-squared = 4.6235, df = 9, p-value = 0.8658
The p-value is > 0.05 meaning the null hypothesis is not rejected (independent values).
It now seems reasonable to move on past basic exploration. There is a question that comes to me. What happens if this test is run many times with newly generated random numbers? Would the same pattern in the small differences consistently occur? I think that might be good for a future, follow-up article.
Random Walk
One other technique used to determine randomness is to see if the values form a random walk3. I initially tried a straight run with the original series and found it boring for experimentation (i.e., a linear view). For a different take, I will shift the values across the axis. Since the values are between 0 and 1, this is a shift of 0.5. To reach -1 and 1, the values will be multiplied by 2. Given the evenness of the distribution, this should create a good balance between positive and negative values. Please note that there are many other techniques that can be used.
Once in the shifted version, a cumulative sum is calculated. This can be seen in the following plot.
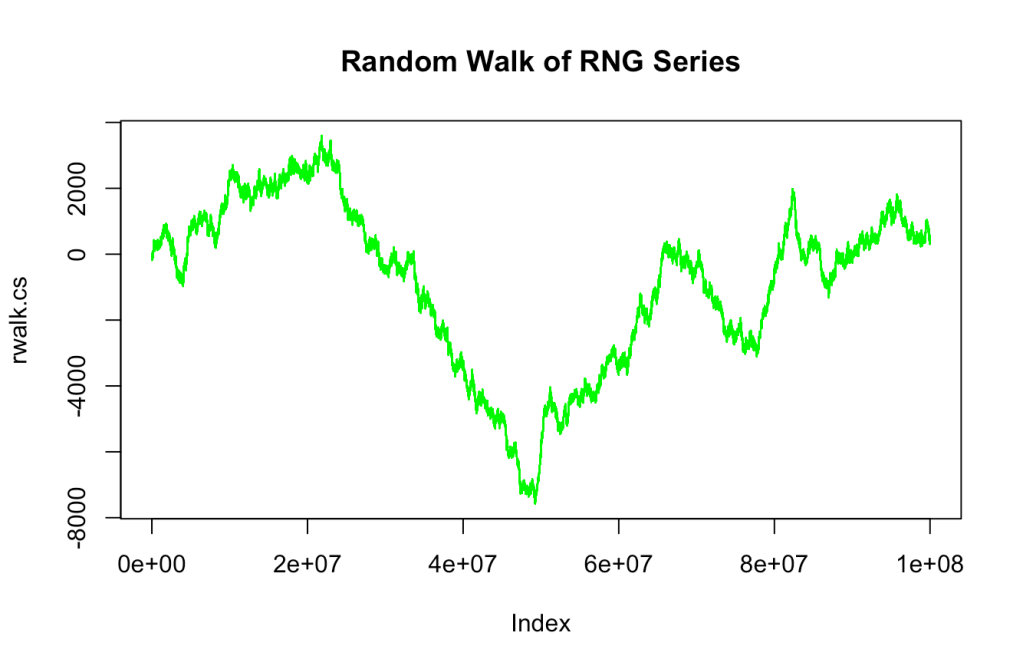
There is a trough in the middle with some interesting directional aspects. Between the different points, there is that “fuzziness” that might be considered a factor of randomness.
ACF and PACF
Does a pattern exist in the series? The Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) tests will show if a correlation occurs between current and previous values. If a correlation does exist, then a pattern might be present. There should be decay noted in the different plots as it moves forward.
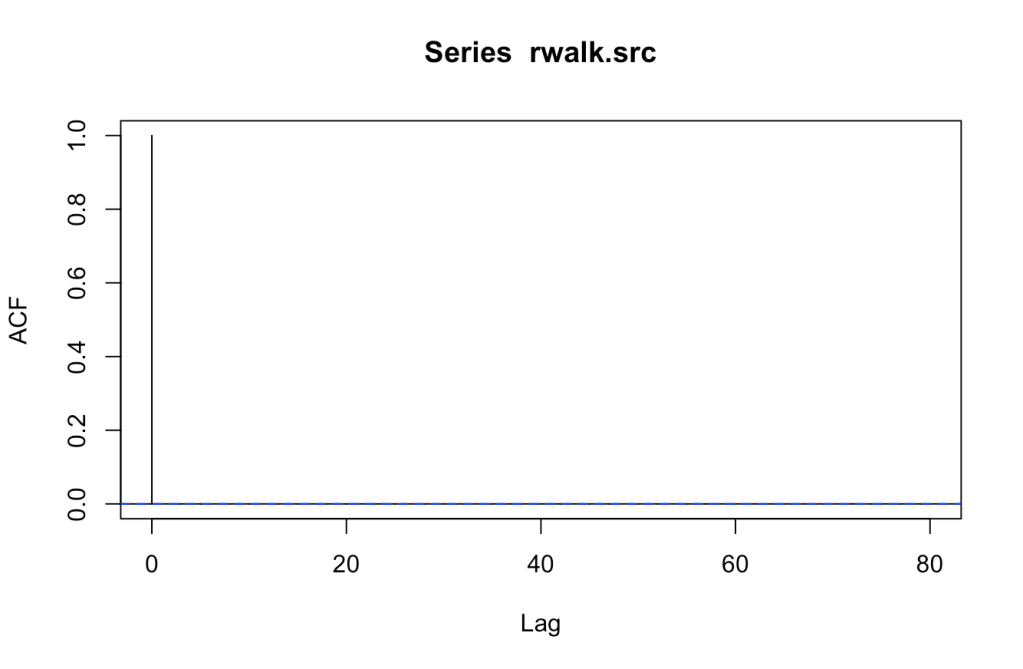
ACF decays quickly. How about PACF?
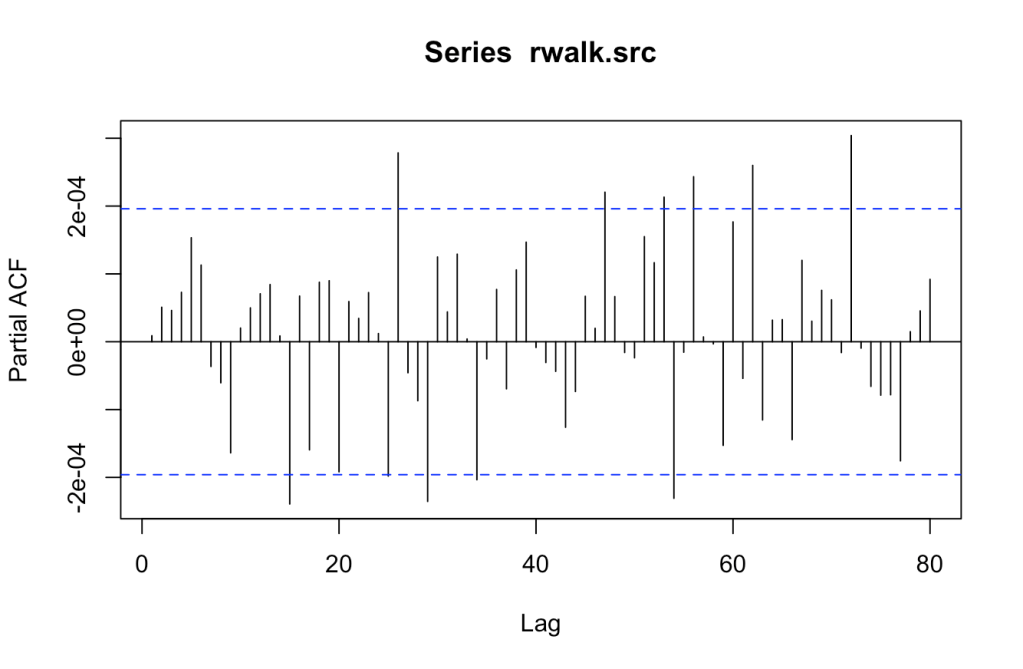
PACF does not looks decaying to me. This is a concern that will need to be considered as analysis progresses.
Augmented Dickey-Fuller Test (ADF)
Another item is to see if there is some type of change in the average as well as the spread. This requires if a test is stationary or not. A stationary series’ properties, such as mean and variance, do not change. The ADF Test is useful here.
In my view, I think that non-stationary series is a better choice for more chaotic effects. Stationary series can be used when controlled scenarios are being simulated (for example, seasonal weather patterns).
To determine if the series is stationary, the Augmented Dickey-Fuller Test (ADF) is run (on the original data set). If the resulting p-value is < 0.05, this will indicate that the set is stationary.
There is an unfortunate note to be shared here. I could not run an ADF Test on the full data set. My laptop could not keep up with the memory requirements. I did execute the test a few times using different parts of the entire set (remember, sampling theory is a good thing to learn). This is not a true test, but the results are consistent.
Augmented Dickey-Fuller Test
data: rwalk[1:1e+06]
Dickey-Fuller = -2.679, Lag order = 99, p-value = 0.2887
alternative hypothesis: stationary
Since the p-value is > 0.05, the null hypothesis is not rejected. This series is non-stationary which is another part of the picture.
With all known information, there seems to be some good base evidence to suggest randomness. I would hope so given the popularity of this RNG. This is not going to be the end. However, I will pause now on direct statistical tests, but you should research other techniques that can be performed (example, look at the randtests libraries in R4). There will certainly be more statistics performed later.
Visual Test
The next test is interesting. I happened to find this approach from some readings on fractal art5. The approach uses visual analysis. The idea behind this is that a graphical pattern will appear out of steps taken that are directed by the random numbers. A pen is put on the drawing surface and moved forward. As each so-called random number is read, the pen is sent in a new direction base on the value. What seems like a disordered scribble (or static) at first, might form patterns over time. If a pattern does form, predictability becomes a concern.
Experiment – Draw the Random Walk
I do not have a pen plotter. Instead, I will use Turtle Graphics. If you are not familiar with Turtle Graphics, please spend time reading on Logo6 as well as the available modern implementations in Python7 and R8. Simply, this functionality allows for easy drawings to be developed using from an algorithm. Think of it as a virtual pen plotter.
Drawing the random walk has simple rules. If the value is negative, go left 90 degrees and forward 1 unit. If the value is positive, go right 90 degrees and forward 1 unit. Repeat till the boundary is hit or the end of list. I could have set the rules where a boundary hit would cause the point to start on the opposite side of the drawing pad but did not. I wanted to capture this condition and the boundary did get hit:
Error in .turtle_draw_error(distance, curX, curY, curAng, curGp, curDraw, :
The Turtle escaped from the terrarium. :-(
This is the resulting picture:

Looking at the way it is developed, there is a trend to the lower right quadrant. I do not see much else except I see how the boxes form. I will need some assistance here.
I want to see if one of the generative AIs can pick up something. This should be interesting as it is comparing the image to quite a large database.
This time, I will choose Bing as Microsoft is really pushing AI these days with Copilot. Here is what it responds when I provide the random walk image and ask, “what do you see?”
“Hello, this is Bing. I can see that you have sent me an image of a map of Italy. I can describe the image for you using my internal tools, but I cannot tell you anything else about it. Do you want me to describe the image for you?”
Of course, I have to say “yes” to this question. Here is the response:
“Okay, here is the description of the image that you sent me:
This is a pixelated image of a map of Italy.
The map is in black and white, with the exception of a small red dot on the southern tip of the country.
The map is not detailed and does not show any cities or landmarks.
The image has a white background.
I hope this helps. Is there anything else I can do for you? 😊”
Somehow, that image looks like Italy to the model. That is interesting it picked up on the shape in this fashion. I did wonder if it would recognize the turtle as part of a turtle which it did not. I would like to know the underlying probabilities it based that summary on.
Let me try another area of the data set.
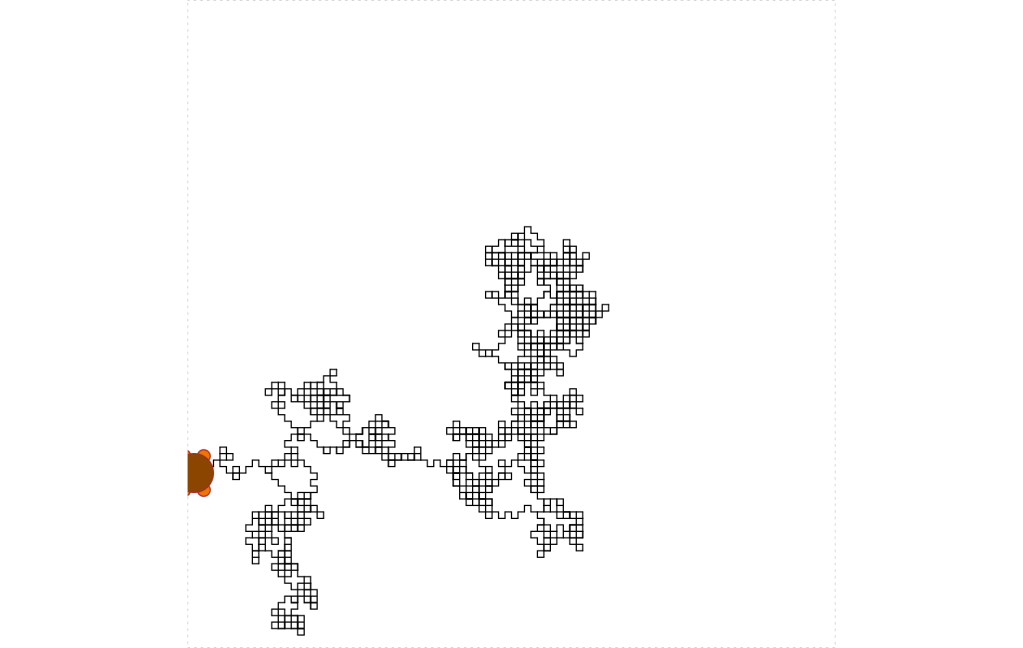
“Hello, this is Bing. I can see that you have sent me an image. I can try to describe it for you using my describe_image tool. Here is what I see:
This is a digital image of a dragon made up of small squares.
The dragon is made up of grey squares with a few white squares scattered throughout.
The dragon has a small orange square for an eye.
The background is white.
The image is pixelated and has a retro video game aesthetic.
I hope this description helps you. Do you want me to do anything else with the image? 😊”
There, see the dragon9? That is a pretty cool explanation of the image. I am not sure I agree with it, but art is in the eye of the beholder.
I will now take a different approach for visual analysis. I will try using a polar co-ordinate plot. If a random walk can generate a pattern in a Cartesian System and generate an interesting result, what about a polar one? Maybe a fractal look will come out of this?
Starting at degree 1 and incrementing 1 degree for each step through the list, use the raw value for a distance from the 0 point. What does that look like?
This will be a bit more challenging. If there are too many data points, then the picture will just get completely covered with no discernible pattern. You can see the results with these 2 pictures. The first one is for 360 degrees. The next is for 1440 degrees.
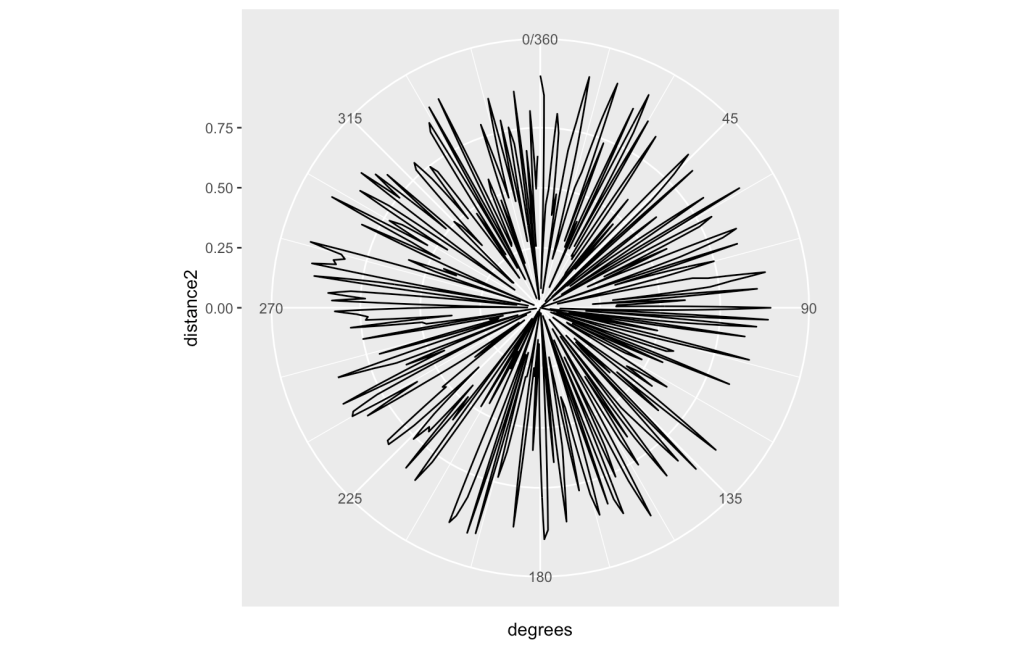
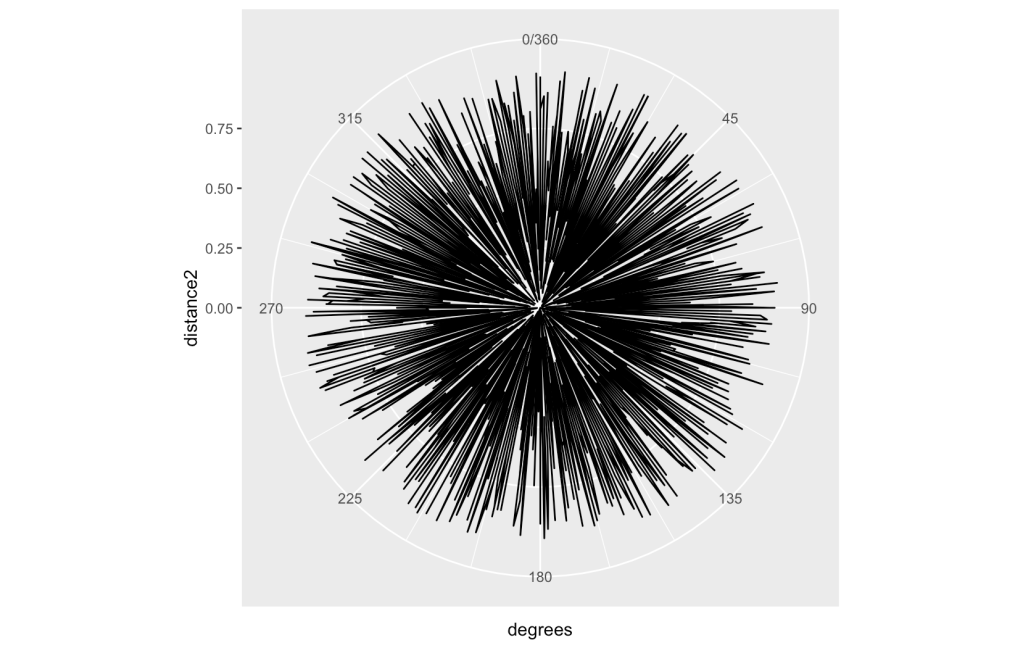
There looks to be a good amount of variability going on. Other attempts with different areas of the set are similar but please experiment as you might find differently. What does Bing’s AI see?
“The overall plot looks like a flower to me. The lines form petals that vary in size and shape. The center of the plot is the center of the flower. The plot is a polar representation of the function r=sin(2θ), which is also known as a rose curve. The number of petals is determined by the coefficient of θ , which is 2 in this case. The length of each petal is determined by the amplitude of the sine function, which is 1 in this case.
I hope this answer helps you understand the plot better. Do you want me to generate a poem about the plot? 😊”
That is very brave to put that equation out for review! Can that formula be used to predict the random number sequence? I will put that to the test in the next article of the series. Still, keep this in mind that there could be a pattern here that might not have been found without a bit of experimentation.
The previous techniques are useful in gaining a good look at the output. However, there is not a core measurement coming out of the tests. It is time to get a bit more advanced and look at a couple of test suites. These have been built with the specific goal of putting a RNG through the paces.
NIST Statistical Test Suite
The National Institute of Standards and Technology (NIST) has created a possible way to determine if a RNG is good or not. The approach has been documented in their publication “A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications.”10
Reading through the documentation, their methodology uses a series of many statistical tests against a stream of numbers output from the RNG to be tested. The results are compiled into a final report for analysis. This is certainly a great way to approach the question. Execute relevant tests in multiple directions to gain a holistic perspective on the subject.
Pay attention to the definition of the null hypothesis for the statistical tests. This is defined in section 1-3 of NIST Documentation where it states:
“the null hypothesis under test is that the sequence being tested is random.”
This caught my attention very quickly. I initially thought that the approach would be that sequences would have to prove their randomness and be defaulted as predictable. When you do your own research, be sure to understand that other tests do follow this definition too.
There is also discussion on predictability of the generated random number sequence and the seed in the NIST Publication. There seems to be an acceptance that PRNGs (Pseudo-RNGs) are considered unpredictable but in varying levels of quality. I would say that is an optimistic view.
The NIST approach is like other statistical tests with the addition that it is trying to create a true standard. This is done by showing a series of resulting p-values. This does not try to hide anything. Instead, it shows how many times the generated sequence becomes predictable or not. We learn that there does not seem to be a final metric to say that the RNG is acceptable or not. Instead, the person analyzing the results is given the information to make this determination. An experiment is necessary to see what we can find.
Experiment – NIST Tests
For this experiment, I had to build the application from the source code. This is straightforward and follows other builds using C11. The result is an application that is old school with text menus. That is fine if it produces useable results and does not take down the system.
The bigger consideration is that there will need to be a file created to the NIST requirements. Where the original approach used a floating-point value, the required file needs contain a series of bits (1s and 0s). I will go back and generate another sequence. I am going to keep this simple and use Python’s random package wrapped by a rounding function. If the float-point values are 0.5 and less, then a 0 is reported. Otherwise, a 1 is generated.
I had to experiment a few times to get the file format to be read by the application correctly. The documentation provides the basic definition. I eventually used the samples in the /data directory as a template from which to build. Once I did that, the tool worked as expected.
It took a few executions of the process to get the feel for the application. Once I did get familiar with the suite, I could run the analysis using many different approaches. You can read through one of the resulting reports in the appendix below. The results suggest that the RNG is good. Remember back to part 1 of this series where experiments show that the same RNG gets a few hits. Maybe the definition of what is good does not equate to a perfect or true RNG?
Again, the suite does not come out with a final Yes or No on the RNG. Instead, it educates the person performing the analysis. It seems it is still up to the individual to determine if the RNG is useful for the application needed. I support this approach. Would any organization say “this is perfect” knowing the possibility of legal responsibilities on making such a statement?
DieHarder
Similar to the NIST efforts, DieHarder12 is a suite of statistical tests used to determine the quality of an RNG. This version is a modern take on the DieHard test suite from the 1990s (interesting note, DieHard is built in Fortran). The various tests utilize the output of the RNG to be tested.
Experiment – RDieHarder
The source code is available for download along with packages. After some unsuccessful experimentation trying to compile and run it under MacOS, I decided to use the version that interfaces directly into R. This is appropriately named “RDieHarder”13 and is straightforward to use. RStudio provides a good interface that makes installation easy.
Fortunately, the previous RNG output file I used in the statistical tests above can be used here. After a very simple call to the rdieharder library, a direct plot is generated using the base settings (‘mt19937’ is the setting for Mersenne Twister). Please note that there are text outputs as well as a nice set of graphical plots as shown here.
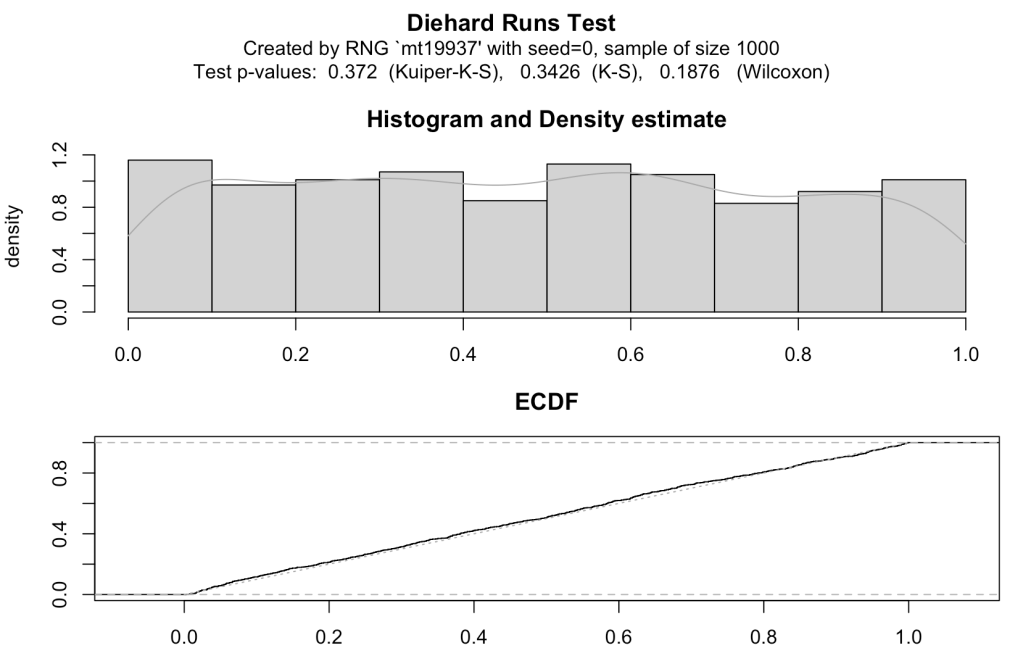
Reading through the output, the histogram shows fairly even distribution. The ECDF (empirical cumulative distribution function) follows a path that suggests a good following of cumulative probability. These both look to be an indication of good results from the RNG.
There is also a way to get the p-value from the test in text format:
Diehard Runs Test
data: Created by RNG `mt19937' with seed=0, sample of size 1000
p-value = 0.372
As in the NIST approach, the null hypothesis is that the data are random. With a p-value of 0.372, the null hypothesis is not rejected meaning the produced data series out of the RNG are random.
There can be further analysis executed using the p-value as an indicator of quality. As the p-value gets closer to 1, the randomness should be stronger. Keep in mind that is a very loose statement I make.
Since this tool is easy to use, many iterations can be done. I merely provide one iteration in this exploration. If you do experiment with this tool, be sure to read through the available documentation as there are numerous parameters that can be set.
The use of suites such as DieHarder and the NIST Statistical Test Suite shows that there is recognition of the need to try to make RNG testing standard. In fact, the information on the DieHarder website states there are efforts to try to incorporate the NIST tests into future releases. At this point, I will end the exploration for now but know this is not the end of what can be done.
Closing Thoughts on RNG Quality
I set out this article to determine a way to ultimately decide on whether a RNG is worth using or not. There certainly are techniques that can be used to assist in that decision. I have not presented an exhaustive list of approaches for identifying quality of RNGs. Still, no one method will give a perfect answer. Why then is there not a single, definitive way of determining RNG quality?
Think about that question back to the thought of using a proper design approach for the system. Is there ever a single, perfect fit for every implementation? If so, why are there so many variations of RNG algorithms?
As an example, would you need the most advanced RNG for a game? That might require more of those precious system resources which could be used for another aspect of the game. In that case, a simple RNG that can be run many times very quickly would be used. Would you pick that simple RNG over an industry standard algorithm for advanced encryption used in a banking system where system resources are all about protection?
Given these considerations, how can a decision be made? Since there is no perfect interpretation of a final “true” or “false” score of some type, how can someone needing a RNG make a proper determination for a given design?
My suggestion would be to take a very holistic approach. The tests are available for public use as are direct statistical tools such as R and Python. These hold great merit by themselves. I would also gather measures on how the target hardware runs the various choices under high load. Generate a meta-score from the different approaches and compare with the system demands.
Going further will probably go too far into system design philosophy. That is not where I want to end this article. Instead, I will propose another question. Would the best scoring for a RNG be to measure how quickly someone can crack it before a required number of tries and time limit?
What can be done with measures and tests suites is very simple. However, it is limited when compared to what a clever human mind can do to break it all. That aspect of RNGs is what I need to experiment with next. That should certainly be exciting!
Thank you and have a great day!
Appendix
Code to generate random number (Python)
# Title: Generate File of Random Numbers
# Author: Andrew Della Vecchia
# Purpose: This simply generates a series of random numbers and saves to a csv file. This is used for RNG quality analysis experiments in article for Andrew's Folly (http://www.andrewsfolly.com)
# Conditions: only use in AS-IS condition. This is completely experimental code with no guarantees.
# packages
import random as rnd
import secrets
import os
import csv
import time
# start timer
execution_time_start = time.perf_counter()
# init
standard_rng_list = []
secrets_rng_list = []
standard_rand = rnd.Random()
secrets_rand = secrets.SystemRandom()
out_path = 'output/'
number_of_randoms = 100000000
standard_out_file_name = os.path.join(out_path, 'standard_rng.csv')
secrets_out_file_name = os.path.join(out_path, 'secrets_rng.csv')
# Generate the random numbers
for x in range(number_of_randoms):
standard_rng_list.append([standard_rand.random()])
secrets_rng_list.append([secrets_rand.random()])
#print(standard_rng_list)
#print(secrets_rng_list)
# write out to file
# standard RNG
standard_rng_file = open(file = standard_out_file_name, mode = 'w+', newline = '')
with standard_rng_file:
standard_write_file = csv.writer(standard_rng_file)
standard_write_file.writerows(standard_rng_list)
# secrets RNG
secrets_rng_file = open(file = secrets_out_file_name, mode = 'w+', newline = '')
with secrets_rng_file:
secrets_write_file = csv.writer(secrets_rng_file)
secrets_write_file.writerows(secrets_rng_list)
# conclude with execution time
execution_time_stop = time.perf_counter()
execution_time_duration = (execution_time_stop - execution_time_start) * 10**6 # microseconds
print(f'Process Completed. Execution Time: {execution_time_duration}')
Code for statistical analysis (R)
# Title: Analysis of RNG output file
# Author: Andrew Della Vecchia
# Purpose: Contains the code for analyzing the output of random numbers from Python RNG calls. This is used for RNG quality analysis experiments in article for Andrew's Folly (http://www.andrewsfolly.com)
# Conditions: only use in AS-IS condition. This is completely experimental code with no guarantees.
# libraries
library(tidyverse)
library(tseries)
# load the RNG output files
source_path <- 'output/'
standard_rng <- read_csv(file.path(source_path, 'standard_rng.csv'), col_names = 'random_number')
# take a general look at the first set of numbers in sequence
head(standard_rng$random_number)
# 5 number summary
standard_rng %>%
summarise(min = min(random_number),
Q1 = quantile(random_number, .25),
median = median(random_number),
mean = mean(random_number),
Q3 = quantile(random_number, .75),
max = max(random_number))
# Standard Deviation
sd(standard_rng$random_number)
# Duplicate values
sum(duplicated(standard_rng$random_number))
tr_rng <- trunc(standard_rng$random_number * 10) /10
# histogram plot
h <- hist(tr_rng)
print(h)
# Independence Test
chisq.test(table(tr_rng))
# random walk
rwalk.src <- (standard_rng$random_number - 0.5) * 2
rwalk.cs <- cumsum(rwalk.src)
plot(rwalk.cs, type = 'l', col = 'green', main = 'Random Walk of RNG Series')
# ACF
rwalk.acf <- acf(rwalk.src)
plot(rwalk.acf)
# PACF
rwalk.pacf <- pacf(rwalk.src)
plot(rwalk.pacf)
# Stationary?
rwalk.adf <- adf.test(rwalk[1:1000000])
print(rwalk.adf)
# Draw the random walk using Turtle
library(TurtleGraphics)
turtle_init()
# go through the random walk values
for (rw_step in rwalk.src[1000000:100000000]) {
# if negative, turn left; otherwise, turn right
if (rw_step < 0) {
turtle_left(90)
} else {
turtle_right(90)
}
# Move the turtle forward
turtle_forward(dist=1)
}
# Polar co-ordinates for random walk
# one step = 1 degree
# value = raw value
rwalk.polar <- standard_rng %>%
mutate(degrees = (row_number() %% 360),
radians = (row_number() %% 360) * pi / 180,
distance1 = (standard_rng$random_number - 0.5) * 2,
distance2 = standard_rng$random_number)
rw_polar_plot <- ggplot(rwalk.polar[1:360,], aes(x=degrees, y=distance2)) +
geom_line() +
# geom_point() +
coord_polar() +
scale_x_continuous(limits = c(0,360),
breaks = seq(0, 360, by = 45),
minor_breaks = seq(0, 360, by = 15)) +
ylim(0, NA)
rw_polar_plot
Code to generate random 1s and 0s (Python)
# Title: Generate File of Random Numbers that are only 0s and 1s for use in NIST STS
# Author: Andrew Della Vecchia
# Purpose: This simple generates a series of random 0s and 1s. The list is saved to a csv file. This is used for RNG quality analysis experiments in article for Andrew's Folly (http://www.andrewsfolly.com)
# Conditions: only use in AS-IS condition. This is completely experimental code with no guarantees.
# packages
import random as rnd
import os
import time
# start timer
execution_time_start = time.perf_counter()
# init
standard_rng_nist_list = []
standard_rand = rnd.Random()
out_path = 'output/'
number_of_randoms = 1004894
standard_out_nist_file_name = os.path.join(out_path, 'standard_nist_rng.txt')
# Generate the random numbers
for x in range(number_of_randoms):
standard_rng_nist_list.append(round(standard_rand.random()))
print(standard_rng_nist_list)
with open(file = standard_out_nist_file_name, mode = 'w+', newline = '') as standard_rng_nist_file:
line_number = 0
list_start_pos = 0
while(list_start_pos <= len(standard_rng_nist_list)):
list_stop_pos = list_start_pos + 23
out_line = ' ' + ''.join(str(rn) for rn in standard_rng_nist_list[list_start_pos:list_stop_pos] ) + '\n'
print(out_line)
standard_rng_nist_file.write(out_line)
line_number += 1
list_start_pos = line_number * 23
# conclude with execution time
execution_time_stop = time.perf_counter()
execution_time_duration = (execution_time_stop - execution_time_start) * 10**6 # microseconds
print(f'Process Completed. Execution Time: {execution_time_duration}')
NIST Experiment Results
------------------------------------------------------------------------------
RESULTS FOR THE UNIFORMITY OF P-VALUES AND THE PROPORTION OF PASSING SEQUENCES
------------------------------------------------------------------------------
generator is <af_data/standard_nist_rng.txt>
------------------------------------------------------------------------------
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 P-VALUE PROPORTION STATISTICAL TEST
------------------------------------------------------------------------------
1 1 0 3 0 2 1 0 1 1 0.534146 9/10 Frequency
0 3 0 0 0 2 2 1 2 0 0.213309 10/10 BlockFrequency
1 2 0 2 1 0 0 1 2 1 0.739918 9/10 CumulativeSums
1 0 1 1 0 1 4 0 2 0 0.122325 9/10 CumulativeSums
1 1 0 2 0 1 3 1 0 1 0.534146 10/10 Runs
2 1 0 0 2 3 1 0 1 0 0.350485 10/10 LongestRun
1 0 2 2 2 1 1 1 0 0 0.739918 10/10 Rank
3 1 0 2 0 1 2 0 1 0 0.350485 10/10 FFT
0 0 0 0 2 2 4 1 0 1 0.066882 10/10 NonOverlappingTemplate
1 0 1 0 1 2 1 1 0 3 0.534146 10/10 NonOverlappingTemplate
0 2 1 0 1 2 1 2 1 0 0.739918 10/10 NonOverlappingTemplate
0 1 0 1 2 1 1 1 1 2 0.911413 10/10 NonOverlappingTemplate
0 0 1 0 1 2 3 0 3 0 0.122325 10/10 NonOverlappingTemplate
1 0 1 1 2 1 2 1 1 0 0.911413 10/10 NonOverlappingTemplate
1 1 1 1 1 0 2 1 1 1 0.991468 10/10 NonOverlappingTemplate
0 2 2 2 1 0 0 2 0 1 0.534146 10/10 NonOverlappingTemplate
0 1 1 1 2 0 2 3 0 0 0.350485 10/10 NonOverlappingTemplate
1 1 1 0 0 2 2 1 1 1 0.911413 10/10 NonOverlappingTemplate
1 3 1 0 1 0 3 0 1 0 0.213309 10/10 NonOverlappingTemplate
1 0 1 0 2 0 0 2 1 3 0.350485 10/10 NonOverlappingTemplate
1 0 1 3 1 1 0 0 0 3 0.213309 10/10 NonOverlappingTemplate
1 1 0 0 0 0 2 2 2 2 0.534146 10/10 NonOverlappingTemplate
1 1 0 0 0 1 1 3 0 3 0.213309 10/10 NonOverlappingTemplate
1 0 2 1 3 1 0 0 1 1 0.534146 10/10 NonOverlappingTemplate
0 1 2 1 1 1 1 2 1 0 0.911413 10/10 NonOverlappingTemplate
1 1 2 1 0 3 0 1 1 0 0.534146 10/10 NonOverlappingTemplate
3 2 1 0 2 1 0 1 0 0 0.350485 10/10 NonOverlappingTemplate
1 0 2 1 0 1 1 1 1 2 0.911413 9/10 NonOverlappingTemplate
1 1 0 2 1 0 0 2 2 1 0.739918 10/10 NonOverlappingTemplate
1 1 1 0 1 2 1 1 1 1 0.991468 10/10 NonOverlappingTemplate
0 0 0 1 1 0 2 4 1 1 0.122325 10/10 NonOverlappingTemplate
3 0 2 3 0 0 0 1 0 1 0.122325 10/10 NonOverlappingTemplate
3 0 0 1 3 1 0 0 1 1 0.213309 10/10 NonOverlappingTemplate
1 1 0 0 1 2 0 1 1 3 0.534146 9/10 NonOverlappingTemplate
3 0 1 1 1 0 1 1 0 2 0.534146 10/10 NonOverlappingTemplate
1 1 0 0 0 2 2 1 1 2 0.739918 10/10 NonOverlappingTemplate
0 2 0 2 0 1 0 2 1 2 0.534146 10/10 NonOverlappingTemplate
1 1 1 0 1 2 0 0 4 0 0.122325 10/10 NonOverlappingTemplate
2 2 1 0 3 0 0 1 1 0 0.350485 10/10 NonOverlappingTemplate
1 1 2 1 1 0 0 0 1 3 0.534146 9/10 NonOverlappingTemplate
0 1 0 1 4 0 0 2 0 2 0.066882 10/10 NonOverlappingTemplate
1 0 0 1 5 1 1 0 1 0 0.017912 10/10 NonOverlappingTemplate
1 1 0 1 0 2 2 2 0 1 0.739918 9/10 NonOverlappingTemplate
2 4 1 0 0 0 1 2 0 0 0.066882 10/10 NonOverlappingTemplate
1 1 1 1 0 1 2 0 1 2 0.911413 10/10 NonOverlappingTemplate
0 1 0 3 0 0 4 0 0 2 0.017912 10/10 NonOverlappingTemplate
1 0 4 1 1 0 1 0 2 0 0.122325 10/10 NonOverlappingTemplate
2 1 2 1 1 1 2 0 0 0 0.739918 10/10 NonOverlappingTemplate
3 0 2 2 1 0 1 1 0 0 0.350485 10/10 NonOverlappingTemplate
0 1 0 1 4 2 1 1 0 0 0.122325 10/10 NonOverlappingTemplate
1 1 0 1 0 1 2 2 2 0 0.739918 10/10 NonOverlappingTemplate
1 1 1 1 1 0 0 4 0 1 0.213309 10/10 NonOverlappingTemplate
1 0 3 0 3 0 1 1 1 0 0.213309 10/10 NonOverlappingTemplate
2 1 2 0 0 0 0 2 1 2 0.534146 10/10 NonOverlappingTemplate
1 1 1 0 2 1 1 2 0 1 0.911413 10/10 NonOverlappingTemplate
1 1 1 1 0 2 1 1 1 1 0.991468 9/10 NonOverlappingTemplate
1 1 1 3 1 1 1 0 1 0 0.739918 10/10 NonOverlappingTemplate
0 1 0 1 1 1 4 0 0 2 0.122325 10/10 NonOverlappingTemplate
3 0 0 0 1 0 3 0 2 1 0.122325 10/10 NonOverlappingTemplate
0 0 2 2 0 0 0 1 5 0 0.004301 10/10 NonOverlappingTemplate
1 1 2 1 1 1 0 1 0 2 0.911413 10/10 NonOverlappingTemplate
0 3 1 2 1 1 1 0 1 0 0.534146 10/10 NonOverlappingTemplate
1 0 2 0 1 0 1 4 0 1 0.122325 9/10 NonOverlappingTemplate
0 0 1 1 0 2 1 2 1 2 0.739918 10/10 NonOverlappingTemplate
0 0 0 1 1 3 1 1 2 1 0.534146 10/10 NonOverlappingTemplate
0 3 2 2 0 0 0 2 1 0 0.213309 10/10 NonOverlappingTemplate
1 1 2 0 0 3 0 0 1 2 0.350485 10/10 NonOverlappingTemplate
2 1 1 3 1 0 1 1 0 0 0.534146 8/10 NonOverlappingTemplate
1 1 1 1 0 0 3 0 2 1 0.534146 10/10 NonOverlappingTemplate
0 0 2 1 0 2 2 0 2 1 0.534146 10/10 NonOverlappingTemplate
1 1 1 0 3 1 2 1 0 0 0.534146 10/10 NonOverlappingTemplate
1 1 2 2 0 0 0 1 3 0 0.350485 9/10 NonOverlappingTemplate
2 1 3 0 0 0 0 1 2 1 0.350485 9/10 NonOverlappingTemplate
1 2 0 1 0 1 1 1 1 2 0.911413 10/10 NonOverlappingTemplate
1 0 1 3 0 1 0 0 2 2 0.350485 9/10 NonOverlappingTemplate
0 1 2 3 0 2 1 0 0 1 0.350485 10/10 NonOverlappingTemplate
1 0 2 1 0 0 1 1 4 0 0.122325 10/10 NonOverlappingTemplate
1 2 1 2 0 1 1 0 0 2 0.739918 10/10 NonOverlappingTemplate
1 1 1 2 1 1 1 0 1 1 0.991468 10/10 NonOverlappingTemplate
1 3 2 0 0 1 0 1 0 2 0.350485 10/10 NonOverlappingTemplate
0 1 1 0 1 0 2 1 3 1 0.534146 10/10 NonOverlappingTemplate
0 1 0 2 1 0 3 0 1 2 0.350485 10/10 NonOverlappingTemplate
0 0 0 0 2 2 4 1 0 1 0.066882 10/10 NonOverlappingTemplate
2 2 1 0 1 0 0 2 1 1 0.739918 9/10 NonOverlappingTemplate
0 2 1 2 0 3 0 2 0 0 0.213309 10/10 NonOverlappingTemplate
1 0 1 0 1 1 1 1 4 0 0.213309 10/10 NonOverlappingTemplate
0 0 1 0 1 1 0 2 3 2 0.350485 10/10 NonOverlappingTemplate
3 1 0 1 1 0 1 0 2 1 0.534146 9/10 NonOverlappingTemplate
1 2 2 1 1 1 2 0 0 0 0.739918 10/10 NonOverlappingTemplate
0 0 0 1 1 1 1 1 3 2 0.534146 10/10 NonOverlappingTemplate
0 2 4 0 1 1 0 1 0 1 0.122325 10/10 NonOverlappingTemplate
1 2 1 1 1 1 0 1 1 1 0.991468 10/10 NonOverlappingTemplate
1 0 1 0 0 2 1 2 1 2 0.739918 10/10 NonOverlappingTemplate
0 1 1 2 0 0 1 1 4 0 0.122325 10/10 NonOverlappingTemplate
0 1 1 2 0 1 2 1 1 1 0.911413 10/10 NonOverlappingTemplate
2 0 2 0 1 2 1 1 1 0 0.739918 10/10 NonOverlappingTemplate
0 0 1 2 0 2 2 1 1 1 0.739918 10/10 NonOverlappingTemplate
0 1 1 2 0 1 1 3 1 0 0.534146 10/10 NonOverlappingTemplate
0 1 1 1 1 0 0 3 1 2 0.534146 10/10 NonOverlappingTemplate
3 1 2 1 1 0 0 1 1 0 0.534146 10/10 NonOverlappingTemplate
1 0 1 0 1 3 1 0 1 2 0.534146 10/10 NonOverlappingTemplate
2 0 1 1 1 1 1 0 1 2 0.911413 9/10 NonOverlappingTemplate
0 2 0 1 1 2 2 1 0 1 0.739918 10/10 NonOverlappingTemplate
2 1 2 1 1 1 1 0 0 1 0.911413 10/10 NonOverlappingTemplate
1 0 1 2 0 3 0 1 0 2 0.350485 10/10 NonOverlappingTemplate
2 1 0 0 2 0 3 0 2 0 0.213309 10/10 NonOverlappingTemplate
3 2 2 1 0 0 1 0 1 0 0.350485 10/10 NonOverlappingTemplate
2 1 1 0 2 3 0 0 1 0 0.350485 10/10 NonOverlappingTemplate
1 0 0 0 1 2 1 1 1 3 0.534146 10/10 NonOverlappingTemplate
1 2 2 2 0 1 0 0 0 2 0.534146 10/10 NonOverlappingTemplate
0 1 2 1 1 1 1 0 1 2 0.911413 10/10 NonOverlappingTemplate
0 1 2 1 2 0 1 0 2 1 0.739918 10/10 NonOverlappingTemplate
1 1 1 1 1 1 0 1 1 2 0.991468 9/10 NonOverlappingTemplate
0 0 2 1 1 1 1 2 1 1 0.911413 10/10 NonOverlappingTemplate
0 0 2 0 1 0 1 3 2 1 0.350485 10/10 NonOverlappingTemplate
2 1 0 1 3 1 2 0 0 0 0.350485 10/10 NonOverlappingTemplate
0 0 2 2 1 1 0 2 1 1 0.739918 10/10 NonOverlappingTemplate
0 1 0 1 2 0 3 1 1 1 0.534146 10/10 NonOverlappingTemplate
0 2 0 0 0 2 1 0 2 3 0.213309 10/10 NonOverlappingTemplate
2 2 1 1 0 0 1 1 1 1 0.911413 10/10 NonOverlappingTemplate
3 0 2 1 0 1 2 1 0 0 0.350485 10/10 NonOverlappingTemplate
1 2 0 0 0 0 1 3 1 2 0.350485 10/10 NonOverlappingTemplate
1 2 2 0 2 0 1 0 1 1 0.739918 10/10 NonOverlappingTemplate
1 1 0 0 0 0 1 0 3 4 0.035174 10/10 NonOverlappingTemplate
1 0 1 1 2 0 3 0 2 0 0.350485 10/10 NonOverlappingTemplate
1 1 0 1 0 3 0 1 1 2 0.534146 10/10 NonOverlappingTemplate
2 0 1 0 1 3 0 2 0 1 0.350485 10/10 NonOverlappingTemplate
2 1 1 1 1 0 1 0 2 1 0.911413 10/10 NonOverlappingTemplate
2 2 0 0 2 0 3 1 0 0 0.213309 10/10 NonOverlappingTemplate
0 2 3 1 1 1 1 0 1 0 0.534146 10/10 NonOverlappingTemplate
0 0 2 2 1 1 0 2 1 1 0.739918 10/10 NonOverlappingTemplate
0 1 1 0 2 1 2 0 2 1 0.739918 10/10 NonOverlappingTemplate
1 1 1 1 0 2 1 2 0 1 0.911413 9/10 NonOverlappingTemplate
1 0 1 2 1 1 2 0 0 2 0.739918 10/10 NonOverlappingTemplate
0 0 2 1 2 0 1 1 2 1 0.739918 10/10 NonOverlappingTemplate
0 0 3 2 0 1 0 0 2 2 0.213309 10/10 NonOverlappingTemplate
1 0 1 2 1 1 2 1 1 0 0.911413 10/10 NonOverlappingTemplate
1 4 1 1 1 0 2 0 0 0 0.122325 10/10 NonOverlappingTemplate
0 3 0 0 2 0 3 2 0 0 0.066882 10/10 NonOverlappingTemplate
1 0 0 2 1 2 1 1 1 1 0.911413 10/10 NonOverlappingTemplate
2 0 1 1 2 1 0 3 0 0 0.350485 10/10 NonOverlappingTemplate
1 2 1 1 2 1 0 0 0 2 0.739918 10/10 NonOverlappingTemplate
1 0 3 1 2 0 0 1 2 0 0.350485 10/10 NonOverlappingTemplate
4 0 1 1 1 1 0 2 0 0 0.122325 10/10 NonOverlappingTemplate
0 0 2 0 2 0 2 2 1 1 0.534146 10/10 NonOverlappingTemplate
1 2 2 1 0 1 1 2 0 0 0.739918 10/10 NonOverlappingTemplate
1 2 1 2 0 1 0 0 2 1 0.739918 10/10 NonOverlappingTemplate
0 0 1 1 5 1 0 1 1 0 0.017912 10/10 NonOverlappingTemplate
0 0 4 0 1 3 0 0 1 1 0.035174 10/10 NonOverlappingTemplate
0 3 0 1 1 0 0 2 0 3 0.122325 10/10 NonOverlappingTemplate
0 2 0 2 0 2 1 1 0 2 0.534146 10/10 NonOverlappingTemplate
2 2 0 0 1 2 1 2 0 0 0.534146 10/10 NonOverlappingTemplate
1 0 1 2 0 1 2 0 0 3 0.350485 10/10 NonOverlappingTemplate
0 1 1 2 1 1 0 0 2 2 0.739918 10/10 NonOverlappingTemplate
0 0 1 2 0 2 3 0 0 2 0.213309 10/10 NonOverlappingTemplate
0 1 0 2 1 0 3 0 1 2 0.350485 10/10 NonOverlappingTemplate
1 0 1 0 2 3 1 0 2 0 0.350485 10/10 OverlappingTemplate
10 0 0 0 0 0 0 0 0 0 0.000000 * 0/10 * Universal
1 0 3 1 1 1 0 2 0 1 0.534146 10/10 ApproximateEntropy
0 0 0 0 0 1 0 0 0 1 ---- 2/2 RandomExcursions
0 0 0 0 0 0 0 1 0 1 ---- 2/2 RandomExcursions
0 0 0 0 1 0 0 0 0 1 ---- 2/2 RandomExcursions
0 0 0 0 0 0 0 0 1 1 ---- 2/2 RandomExcursions
0 0 1 0 0 1 0 0 0 0 ---- 2/2 RandomExcursions
0 0 1 0 0 0 0 1 0 0 ---- 2/2 RandomExcursions
0 1 0 0 0 0 1 0 0 0 ---- 2/2 RandomExcursions
0 1 0 0 0 0 0 0 0 1 ---- 2/2 RandomExcursions
0 1 0 0 1 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 1 1 0 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 1 0 0 0 1 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 0 1 0 0 0 0 1 ---- 2/2 RandomExcursionsVariant
0 0 1 0 0 0 1 0 0 0 ---- 2/2 RandomExcursionsVariant
0 1 0 0 1 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
1 0 0 0 1 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 1 1 0 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 0 0 1 0 0 0 1 ---- 2/2 RandomExcursionsVariant
1 0 0 0 0 0 0 1 0 0 ---- 2/2 RandomExcursionsVariant
1 0 0 0 0 0 0 0 1 0 ---- 2/2 RandomExcursionsVariant
0 1 0 0 0 0 0 0 1 0 ---- 2/2 RandomExcursionsVariant
0 0 1 0 0 0 1 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 1 0 0 1 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 0 0 1 1 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 1 0 0 1 0 0 0 ---- 2/2 RandomExcursionsVariant
0 1 0 0 1 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 1 1 0 0 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 1 2 1 2 1 0 2 1 0 0.739918 10/10 Serial
0 1 2 1 3 1 1 0 1 0 0.534146 10/10 Serial
0 1 1 3 0 2 1 1 0 1 0.534146 10/10 LinearComplexity
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The minimum pass rate for each statistical test with the exception of the
random excursion (variant) test is approximately = 8 for a
sample size = 10 binary sequences.
The minimum pass rate for the random excursion (variant) test
is approximately = 1 for a sample size = 2 binary sequences.
For further guidelines construct a probability table using the MAPLE program
provided in the addendum section of the documentation.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
References
[1] George Pipis. R-Bloggers.How to Test for Randomness.11/15/2020. Retrieved from: https://www.r-bloggers.com/2020/11/how-to-test-for-randomness/
[2] Raj Jain. Testing Random-Number Generators. 2008. Retrieved from https://www.cse.wustl.edu/~jain/cse567-08/ftp/k_27trg.pdf
[3] Biskup, Marek. PCMI Notes, Part 1. Department of Mathematics, University of California, Los Angeles. Chapter 2 – Random Walks. Retrieved from: https://www.math.ucla.edu/~biskup/PDFs/PCMI/PCMI-notes-1
[4] Frederico Caeiro ORCID iD [aut, cre], Ayana Mateus. Package ‘randtests.’ 06/20/2022. Retrieved from: https://cran.r-project.org/web/packages/randtests/index.html
[5] Jennifer Lowery. What is Fractal Art? 02/25/2022. Retrieved from: https://study.com/learn/lesson/fractal-art-overview-examples.html
[6] Logo Foundation, MIT. Logo History. 2015. Retrieved from: https://el.media.mit.edu/logo-foundation/what_is_logo/history.html
[7] Python Software Foundation. Turtle – Turtle graphics. Oct 15, 2023. Retrieved from: https://docs.python.org/3/library/turtle.html
[8] Anna Cena, Marek Gagolewski, Barbara Zogala-Siudem, Marcin Kosinski, Natalia Potocka, Barbara Zogala-Siudem. Package ‘TurtleGraphics.’ 02/14/2018. Retrieved from: https://cran.r-project.org/web/packages/TurtleGraphics/TurtleGraphics.pdf
[9] Homestar Runner Wiki. Trogdor. July 14, 2023. Retrieved from: http://www.hrwiki.org/wiki/Trogdor
[10] National Institute of Standards and Technology. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. 04/2010. Retrieved from: https://csrc.nist.gov/pubs/sp/800/22/r1/upd1/final
[11] NIST – GitHub. The NIST Statistical Test Suite. 07/2022. Retrieved from: https://github.com/terrillmoore/NIST-Statistical-Test-Suite#test-input-scripts
[12] Robert G. Brown. Robert G. Brown’s General Tools Page – dieharder. 03/06/2020. Retrieved from: https://webhome.phy.duke.edu/~rgb/General/dieharder.php
[13] Dirk Eddelbuettel, Robert G Brown, David Bauer. RDieHarder: R Interface to the ‘DieHarder’ RNG Test Suite. Retrieved from: https://cran.r-project.org/web/packages/RDieHarder/index.html
One response to “An Exploration of Random Numbers – Part 2: Quality”
[…] leads us to remember how diverse RNG algorithms can be. There are some analysis techniques being used alongside numerous efforts to create a standard set of…. I will remind everyone here that there are no true standards but plenty of good, scientific tests […]
LikeLike